Probabilidad: Es la posibilidad de que ocurra un evento en ciertas condiciones.
Interpretaciones de probabilidad:
- Percepción: se puede predeteminar un evento basándose en experiencias anteriores.
- Clásica: se pueden conocer los resultados de un experimento sin necesidad de llevarlo a cabo.
- Frecuentista: podemos saber la probabilidad de un suceso después de repetir y observar varias veces el experimento.
Experimento aleatorio
Es aquel que proporciona diferentes resultados aún cuando se repita siempre de la misma manera.
Espacio muestral
es el conjunto de los posibles resultados de un experimento aleatorio. Se denota por la letra S.
Ejemplo:
- S={s,a,a,s,a,s,s,a,s,s} Espacio muestral de lanzar una moneda 10 veces.
- S={1,2,3,4,5,6} Espacio muestrald e lanzar un dado (una vez).
Evento
subconjunto del espacio muestral. Se toman sólo los elementos necesarios del espacio muestral que cumplan alguna condición dada.
Permutaciones
El número de permutaciones de n objetos es el número de formas en los que pueden acomodarse esos objetos en términos de orden.
El número de permutaciones de n objetos tomados r a la vez, donde r es menor que n es igual a:
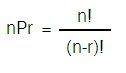Combinaciones
En el caso de las combinaciones, lo importante es el número de agrupaciones diferentes de objetos que pueden incurrir sin importar su orden. Por lo tanto en las combinaciones se busca el número se subgrupos diferentes que pueden tomarse a partir de n objetos.
El número de combinaciones de n objetos tomados r a la vez es igual a:
Diagramas de árbol:
Un diagrama de árbol es una representación gráfica de un experimento que consta de r pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.
___________________________________________________________________
Experimento: Lanzar un dado 2 veces.
S={ (1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
Existen 36 resultados posibles.
Mostrar la probabilidad ( P( ) ) de que la suma de los dos dados sea 5
S={(1,4),(2,3),(3,2),(4,1)}
P(5) = 4/36 = 1/9
___________________________________________________________________
Ejercicio 1
Considere un experimento en el que cada 10 minutos se verifica el volúmen de llenado de envases de refresco de una máquina llenadora automática, con la finalidad de saber si el producto cumple con las especificaciones de la cantidad de llenado.
Encontrar el espacio muestral.
- La evaluación se realiza hasta encontrar una lata que no cumpla las especificaciones; entonces el espacio muestral, en cada elemento incluye el numero posible de latas que si cumplen las condiciones de llenado, hasta encontrar la lata que no lo haga.
n = no cumple las especificaciones de llenado
S={n, sn, ssn, sssn, ssssn, . . . . . , (xs)n}
El espacio muestral comienza con (n) pensando en que sea posible no encontrar ningun envase que cumpla con las especificaciones. De ahí en adelante, se comienza a agregar una lata (s) en cada elemento del espacio muestral.
En este ejercicio el espacio muestral resulta en infinito ya que no hay una cantidad definida de latas (s) antes de encontrar una lata (n).
