Probabilidad Y Estadistica: octubre 2008

martes, octubre 14

Regla de la Multiplicación

Si A y B son independientes:

-P(A int B) = P(B)P(A|B)

-P(B int A) = P(A)P(B|A)

Si A y B son dependientes:

-P(A int B) = P(A)P(B)

_______________________________________________________________________________

Se lanzan un dado blanco y un dado negro. Encontrar la probabilidad de que la suma de sus caras sea 7 y que el numero del dado negro sea mayor que eld el dado blanco.

Sean los eventos:

A={la suma de las caras es 7}
B={dado negro mayor a dado blanco}

P(A)= 6/36 = 1/6
P(B)= 16/36

P(A|B)= 3/15

P(A int B)= (3/15)(15/36) = 3/36 = 1/12

Probabilidad Condicional Y Teorema de Bayes

Es la probabilidad de que ocurra un evento considerando dentro de la probabildiad de otro evento dado.

Se indica así P(A|B), lo cual siginifica que queremos obtener la probabilidad de A a partir de la probabilidad de B. (A dado B)}

Dos eventos son independientes cuando la probabilidad de uno no influencia la probabilidad del otro.
"Independencia de eventos es lo mismo que eventos mutuamente exclusivos"

_________________________________________________________________________________

Ejemplo. (Suma de las caras de dos dados).

Sean los eventos:

A={suma es 10 u 11} = { (4,6),(5,5),(5,6),(6,4),(6,5) }
B={caras iguales} = { (1,1),(2,2),(3,3),(4,4),(5,5),(6,6) }

Cuál es la probabilidad de B dado A?

P(B|A) = P(A int B)/P(A) = (1/36)/(5/36) = 1/5 = 0.2

_________________________________________________________________________________

Una variante al ejemplo anterior.

A={suma es 10} = { (4,6),(5,5),(6,4) }
B={caras iguales} = { (1,1),(2,2),(3,3),(4,4),(5,5),(6,6) }

P(A) = 3/36
P(B) = 6/36

P(A|B) = 1/6

P(B|A) = 1/3

Los dos eventos son independientes.

Teorema de Bayes

Si A₁, A₂,... , A_n son:

Sucesos incompatibles 2 a 2.

Y cuya unión es el espacio muestral (A₁ A₂ ... A_n = E).

Y B es otro suceso.

Resulta que:

Las probabilidades p(A₁) se denominan probabilidades a priori.

Las probabilidades p(A_i/B) se denominan probabilidades a posteriori.

Las probabilidades p(B/A_i) se denominan verosimilitudes.

________________________________________________________________________________

Ejemplo:

La probabilidad de que haya un accidente en una fábrica que dispone de alarma es 0.1. La probabilidad de que suene esta sí se ha producido algún incidente es de 0.97 y la probabilidad de que suene si no ha sucedido ningún incidente es 0.02.

En el supuesto de que haya funcionado la alarma, ¿cuál es la probabilidad de que no haya habido ningún incidente?

Sean los sucesos:

I = Producirse incidente.

A = Sonar la alarma.

árbol

Ejercicios (Regla de la Adición)

Cuál es la probabilidad de obtener un total de 7 u 11 cuando se lanza un par de dados?

s(7)={ (1,6),(2,5),(3,4),(6,1),(5,2),(4,3) }
s(11)={ (5,6),(6,5) }

P(7)= 6/36 = 1/6

P(11)= 2/36

____________________________________________________________________________________

Si las pobabilidades de alguien que compra un auto para elegir un color entre Verde, Blanco, Rojo o Azul, son respectivamente 0.9, 0.15, 0.21, 0.23.

Cual es la probabildiad de que un comprador adquiera un automovil que tenga uno de esos colores.

P(V U B U R U A)= 0.9+0.15+0.21+0.23 = 0.68

Los eventos son independientes. Ya que no hay intersecciones (el auto no puede tener dos colores), simplemente se suman las probabilidades de cada color disponible para el automovil.

.

Regla de la Adición

Los eventos compuestos se generan al aplicar operaciones básicas. Las intersecciones, las uniones y los complementos son de interés frecuente.

La probabilidad de un evento compuesto a menudo puede obtenerse a partir de las probabilidades de cada uno de los eventos que lo forman. En ocaciones, las operaciones básicas de los conjuntos son útiles para determinar la probabilidad de un evento compuesto.

-Regla de la adición:

P(A int B) = P(A)+P(B) <------si es independiente

P(A U B) = P(A)+P(B)-P(A int B) <--------si es dependiente

-Cuando se tienen más de 3 eventos:

P(A U B U C)= P(A) + P(B) + P(C) - P(A int B) - P(A int C) - P(B int C) - P(A int B int C)

-Si los eventos son mutuamente excluyentes:

(A int B int C) = 0
P(A int B int C) = P(A) + P(B) + P(C)

___________________________________________________________________________________

Ejemplo.

La siguiente tabla presenta la historia de 940 obleas.

Supóngase que se elige al azar una oblea.
Sean los eventos:

A={altos niveles de contaminación}
B={la oblea está en el centro del instrumento}

a) Interpretar . (A U B) y (A int B)

n(A)=358
n(B)=314
n(A int B)=246
n(A U B)= n(A)+n(B)-n(A int B)= 358+314-246= 426

b) Calcule la probabilidad de cada evento

P(A)= 358/940 = 0.38

P(B)= 314/940 = 0.32

P(A U B)= 426/940 = 0.45

P(A int B)= 246/940 = 0.26

.

Axiomas de Probabilidad

Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función que definimos sobre unos sucesos determine consistentemente valores de probabilidad sobre dichos sucesos.

Axioma 1
La probabilidad de un suceso

A un número entero positivo

mayor o igual que 0.

$P(A) \geq 0$

Axioma 2
La suma de las probabilidades de todos los elementos en el espacio muestral debe ser siempre igul a 1. Nunca más ni menos.

$P(\Omega) = 1\!$

Axioma 3
Si A₁, A₂... son sucesos mutuamente excluyentes , entonces:

$P(A_1 \cup A_2 \cup \cdots) = \sum P(A_i)$ .

Según este axioma se puede calcular la probabilidad de un suceso compuesto de varias alternativas mutuamente excluyentes sumando las probabilidades de sus componentes.

El valor de la probabilidad de cualquier evento, debe encontrarse entre 0 y 1

0<= P(E) <= 1

Para dos eventos E1 y E2 con (E1 int E2)=0

P(E1 U E2)= P(E1)+P(E2)

P(0)=0

Si E es un evento cualquiera.....

P(E')=1-P(E)

Ejemplos de Probabilidad

Ejemplo 1

Sean los eventos:

E1={x|1<=x<10}
E2={x|3
Encuentre (E1 U E2), (E1 interseccion E2), E', (E' interseccion E2).

E1 U E2 = {1,2,3,4,.....118} = {x|1<=x<=11)

E1 interseccion E2 = {4,5,6,7,8,9} = {x|4<=x<=9}

E' = {10,11,12,.....} = {x|x>=10}

E' interseccion E2 = {10,11,12,.....118} = {x|10<=x<=118}

_______________________________________________________________________________

Ejemplo 2

Se realizan pruebas de policarbonato y se prueba su resistencia a las rayaduras y a los golpes, clasificándolos en Alta o Baja. Los resultados fueron lo siguientes:

........................Resistencia a golpes

..................... ......Alta.......Baja

Resistencia... Alta. .. 40......... 4 ......44
a rayaduras... Baja. .. 2 ........ 3 .......5
.---------------------------------------------
.................................42......... 7 ......49

Sean los eventos:

A={alta resistencia a los golpes}
B={alta resistencia a las rayaduras}

Determinar: (A int B), A', A U B.

A int B = 40
A' = 7
A U B = 46

_______________________________________________________________________________

Ejmplo 3

Se toman muestras de una pieza de aluminio fundido y se clasifican según su función con la superficie (en micropulgadas) y con las mediciones de su longitud. A continuación se resumen los resultados obtenidos con 100 muestras.

............................................Longitud

.......................................Excelente.....Buena

Acabado de....Excelente.........75 ........ 7 .........82
superficie........Buena ............10 ........... 8 .........18
.---------------------------------------------------
..........................................85 .......... 15..........100

Sean los eventos:

A={la muestra tiene un acabado excelente}
B={la muestra tiene una longitud excelente}

Determine el número de muestras en:

A' int B = 10
B' = 15
A U B = 92

_______________________________________________________________________________

Ejemplo 4

Los resultados posibles de un experimento son {a,b,c,d} con probabilidad 0.1,0.3,0.5 y 0.1 respectivamente.

Sean los eventos:

A = {a,b}
B = {b,c,d}
C = {d}

Encuentre:

1. P(A) = ............ 0.4 = 40%

2. P(B) = ............ 0.9 = 90%

3. P(C) = ............ 0.1 = 10%

4. P(A') =............ 0.6 = 60%

5. P(B') =............ 0.1 = 10%

6. P(C') =............ 0.9 = 90%

7. P(A int B) = ...... 0.3 = 30%

8. P(A U B) = ........ 1.0 = 100%

9. P(A' int B) =...... 0.6 = 60%

10. P(B' int A)= ..... 0.1 = 10%

sábado, octubre 11

Probabilidad - UNIDAD II

Conceptos:

Probabilidad: Es la posibilidad de que ocurra un evento en ciertas condiciones.

Interpretaciones de probabilidad:

Percepción: se puede predeteminar un evento basándose en experiencias anteriores.
Clásica: se pueden conocer los resultados de un experimento sin necesidad de llevarlo a cabo.
Frecuentista: podemos saber la probabilidad de un suceso después de repetir y observar varias veces el experimento.

Todos los elementos de una muestra tienen la misma porbabilidad de ser seleccionados. No existe "sesgo" o preferencia por algun de los elementos.

Experimento aleatorio

Es aquel que proporciona diferentes resultados aún cuando se repita siempre de la misma manera.

Espacio muestral

es el conjunto de los posibles resultados de un experimento aleatorio. Se denota por la letra S.

Ejemplo:

S={s,a,a,s,a,s,s,a,s,s} Espacio muestral de lanzar una moneda 10 veces.

S={1,2,3,4,5,6} Espacio muestrald e lanzar un dado (una vez).

Evento

subconjunto del espacio muestral. Se toman sólo los elementos necesarios del espacio muestral que cumplan alguna condición dada.

Permutaciones

El número de permutaciones de n objetos es el número de formas en los que pueden acomodarse esos objetos en términos de orden.
El número de permutaciones de n objetos tomados r a la vez, donde r es menor que n es igual a:

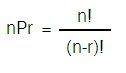Combinaciones

En el caso de las combinaciones, lo importante es el número de agrupaciones diferentes de objetos que pueden incurrir sin importar su orden. Por lo tanto en las combinaciones se busca el número se subgrupos diferentes que pueden tomarse a partir de n objetos.

El número de combinaciones de n objetos tomados r a la vez es igual a:

Diagramas de árbol:

Un diagrama de árbol es una representación gráfica de un experimento que consta de r pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.

___________________________________________________________________

Experimento: Lanzar un dado 2 veces.

S={ (1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}

Existen 36 resultados posibles.

Mostrar la probabilidad ( P( ) ) de que la suma de los dos dados sea 5

S={(1,4),(2,3),(3,2),(4,1)}

P(5) = 4/36 = 1/9

___________________________________________________________________

Ejercicio 1

Considere un experimento en el que cada 10 minutos se verifica el volúmen de llenado de envases de refresco de una máquina llenadora automática, con la finalidad de saber si el producto cumple con las especificaciones de la cantidad de llenado.
Encontrar el espacio muestral.

La evaluación se realiza hasta encontrar una lata que no cumpla las especificaciones; entonces el espacio muestral, en cada elemento incluye el numero posible de latas que si cumplen las condiciones de llenado, hasta encontrar la lata que no lo haga.

s = si cumple las especificaciones de llenado
n = no cumple las especificaciones de llenado

S={n, sn, ssn, sssn, ssssn, . . . . . , (xs)n}

El espacio muestral comienza con (n) pensando en que sea posible no encontrar ningun envase que cumpla con las especificaciones. De ahí en adelante, se comienza a agregar una lata (s) en cada elemento del espacio muestral.

En este ejercicio el espacio muestral resulta en infinito ya que no hay una cantidad definida de latas (s) antes de encontrar una lata (n).

miércoles, octubre 8

Datos Agrupados

Pasos para agrupar datos

Definir el rango
Calcular el número de clases
Calcular el ancho de cada clase
Determinar los intervalos

rango = valormaximo - valor minimo

no.clases = √n

ancho = rango / no.clases

Si utilizamos el ejemplo mostrado anteriormente,

97, 105, 181, 134, 151, 153, 154, 154,
157, 160, 163, 174, 175, 178, 180, 183,
190, 196, 199, 207, 218, 221, 228, 245.

podemos obtener los siguientes valores para datos agrupados:

rango = 245 - 97 = 148

no.clases = √25 = 5
ancho = 148 / 5 = 29.6 ≈ 30

Ahora se acomodan los datos clasificándolos en cada intervalo:

Intervalos de clase	ƒrec.	Marca de clase	ƒ*Marca de clase
95 ≤ x <>	2	110	220
125 ≤ x <>	6	140	840
155 ≤ x <>	8	170	1340
185 ≤ x <>	5	200	1000
215 ≤ x < 245	4	230	920
			Σ=4340

= 4340/25 = 173.6

Nótese que el espacio dentro de cada intervalo es de 30.

Ya teniendo datos agrupados se puede obtener otra información, como la frecuencia, las Marcas de clase, y la media aritmética.
A partir de estos, es posible crear diagramas que representen los datos gráficamente.

martes, octubre 7

Diagramas

Cuando tenemos datos agrupados existen diferentes formas de representar gráficamente los datos o resultados de una investigación. Dependiendo de los tipos de datos que se quieren mostrar se puede usar:

Histograma